Авторы: Котов А.В.
ЦЕЛЬ РАБОТЫ
1. освоить основные способы и функции работы с векторами и матрицами в системе MathCAD; 2. освоить основные приемы работы и форматирования с 2D и 3D графиками в системе MathCAD; 3. освоить приемы решения систем линейных и нелинейных уравнений в системе MathCAD.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Рассматриваемые в последующих лабораторных работах математические модели 2D и 3D рычажных механизмов сельскохозяйственных машин основаны на элементарных знаниях векторного анализа и векторного преобразования координат с последующей реализацией этих знаний при помощи современных систем автоматизированного проектирования. Поэтому в данной лабораторной работе рассмотрены основные понятия и определения векторной алгебры и способы их реализации в математическом пакете MathCAD.
В векторной алгебре различают две основные величины – векторные и скалярные. Дадим определение этим двум величинам.
Скаляром называется величина, которая может быть охарактеризована одним числом, выражающим отношение этой величины к соответствующей единице измерения.
Вектором называется направленный отрезок, который характеризуется следующими элементами: начальной точкой («точкой приложения»), направлением и длиной («модулем вектора»). Всякий вектор содержит в себе скалярную величину и может быть изображен с помощью прямолинейного отрезка, у которого различают начало и конец.
К частным случаям векторов можно отнести:
единичный вектор e или так называемый орт – вектор, длина которого равна единице;
нулевой вектор 0 – вектор, длина которого равна нулю.
Любой вектор можно представить в виде проекций на координатные оси выбранной системы координат. На рисунке 1.1 представлено графическое разложение вектора AB на проекции в пространственной системе координат и математическая запись данного вектора.
Рисунок 1.1 – Графическое представление вектора
Всякий вектор a может быть представлен в виде произведения единичного вектора (имеющего направление, совпадающее с вектором a) на длину (модуль) вектора a, т.е.:
где ea – единичный вектор направления вектора a; |a| – модуль вектора a.
Различают следующие типы векторов:
свободный вектор – вектор, который можно переносить параллельно самому себе и прилагать в любой точке, при условии сохранения его длины и направления;
скользящий вектор – вектор, который можно переносить по прямой, определяющей направление этого вектора;
связанный вектор – вектор, который относится к определенной точке.
Равными называются два вектора если они расположены на параллельных или совпадающих прямых, имеют одинаковую длину и одинаково направлены.
Радиус-вектор некоторой точки пространства называется вектор, идущий от начала выбранной системы координат к данной точке.
Положение вектора в пространстве непосредственно связано с выбранной системой координат. Если три взаимно перпендикулярные оси в трехмерном пространстве, исходящие из общей точки, образуют правую тройку (правую систему координат), т.е. ориентированы по правилу буравчика, то три взаимно перпендикулярные плоскости, проходящие через соответствующие оси, называются координатными плоскостями. В таком случае говорят о декартовой системе координат трехмерного пространства. В последующих лабораторных работах все вектора будут заданы в правой декартовой 2D или 3D системе координат.
К векторам применимы операции сложения и вычитания.
Сложение векторов может осуществляться по следующим правилам:
Разностью векторов OE и OB называется такой вектор EB, который при сложении с вектором OE дает вектор OB:
Графическое построение вектора EB можно осуществить следующим образом. От произвольной точки пространства откладывается два вычитаемых вектора OE и OB. Их разностью будет вектор EB, начало которого совпадает с концом вычитаемого вектора OE, а конец его – с концом уменьшаемого вектора OB (см. сложение векторов по правилу треугольника).
Скалярным произведением двух векторов a и b называется число, равное произведению их длин на косинус угла между ними:
Различают геометрический и физический смысл скалярного произведения (см. рисунок 1.2):
геометрический смысл: скалярное произведение вектора a на единичный вектор eb равно проекции вектора a на направление единичного вектора eb;
физический смысл: если вектор a изображает силу, точка приложения которой перемещается из начала в конец вектора b, то скалярное произведение данных векторов равно работе указанной силы.
а) б)
а – геометрический смысл; б – физический смысл
Рисунок 1.2 – Скалярное произведение
Для скалярного произведения характерно следующее свойство: два вектора a и b перпендикулярны, тогда и только тогда, когда их скалярное произведение равно нулю, т.е. a·b=0.
Векторным произведением двух векторов a на b называется вектор c, который направлен перпендикулярно плоскости перемножаемых векторов в ту сторону, откуда поворот от первого сомножителя ко второму на меньший угол виден против хода часовой стрелки (если все три вектора приведены к общему началу) и имеет модуль равный произведению длин перемножаемых векторов на синус угла между ними:
Различают геометрический и физический смысл векторного произведения (см. рисунок 1.3):
геометрический смысл: модуль векторного произведения двух векторов равен площади параллелограмма, построенного на этих векторах;
физический смысл: если вектор F изображает силу, приложенную в точке B, то векторное произведение вектора AB на вектор-силу AB×F выражает момент силы F относительно точки A. Направление вектора M – вектора момента определяется по правилу буравчика.
а) б)
а – геометрический смысл; б – физический смысл
Рисунок 1.3 – Векторное произведение
Для векторного произведения характерно следующее свойство: два вектора a и b параллельны, тогда и только тогда, когда их векторное произведение равно нулю, т.е. a×b=0.
Создание векторов и матриц в системе MathCAD
Вектора и матрицы в системе MathCAD имеют тот же смысл, что и в классической математике. К ним существует два вида доступа: как к единому объекту и как к элементу.
Для задания векторов и матриц можно либо воспользоваться комбинацией «горячих клавиш» (см. ниже), либо нажать на соответствующей кнопке с изображением шаблона матрицы.
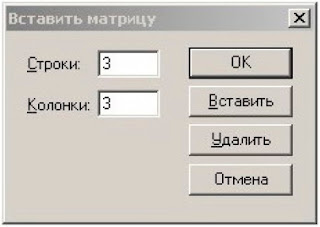
Любое из этих действий вызывает появление диалогового окна (см. рисунок 1.4) в котором надо указать размер матрицы, т.е. количество ее строк m и столбцов n.
Рисунок 1.4 – Диалоговое окно создания матрицы
Для векторов (представляющих собой одномерный массив) один из этих параметров должен быть равен 1. При m=1 получили вектор-столбец, а при n=1 – вектор строку. Матрицы является двумерным массивом с числом элементов m×n.
После задания соответствующих строк и столбцов на экране появится таблица для ввода данных, например:
задание вектора 3×1: задание матрицы 3×3
Местоположение и доступ элемента задается одним индексом для вектора или двумя индексами для матрицы. Используя нижний индекс можно не только извлекать элемент из матрицы (вектора), но и сформировать его. Нижняя граница индексации определяется системной переменной ORIGIN, которая может принимать значения 0 и 1 (по умолчанию ее значение равно 0). Индексы могут быть только целыми положительными числами (и нулем).
Помимо нижних индексов в системе MathCAD существуют и верхние индексы, которые позволяют в более компактной форме работать со столбцами матрицы – извлекать или формировать их.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Исходные данные
Исходные данные к каждой лабораторной работе зависят от номера варианта студента по списку в журнале и второй цифры в номере группы студента. Для примера все рассматриваемые лабораторные работы будут рассчитаны для номера студента по списку в журнале 30 и группы С-31, для чего вводится вспомогательная переменная:
В последующих лабораторных работах данная переменная больше не будет вводиться в работу, но будет предполагаться уже заданной.
В данной лабораторной работе рассмотрим основные матричные (векторные) операторы и функции в системе MathCAD, придерживаясь следующих обозначений: для векторов – V, для матриц M, для скалярных величин – Z. Введем исходные данные согласно принятым условным обозначениям:
1. Сложение двух векторов:
2. Вычитание двух векторов:
3. Вычитание из всех элементов вектора скаляра:
4. Смена знака у элементов векторов и матриц:
5. Умножение вектора (матрицы) на скаляр:
6. Деление всех элементов вектора (матрицы) на скаляр:
7. Скалярное умножение двух векторов:
8. Векторное умножение двух векторов:
9. Умножение матрицы на вектор:
10. Обратная матрица:
11. Транспонирование вектора (матрицы):
12. Вычисление модуля вектора и определителя матрицы:
13. Вычисление суммы элементов вектора:
14. Выделение столбца и строки из матрицы:
выделение целого столбца выделение целой строки
15. Выделение элемента из вектора (матрицы):
элемента столбца элемента матрицы
16. Создание произвольного вектора из n элементов (в данном примере из 3-ех элементов) со значением в заданных пределах (в данном примере в диапазоне чисел от 0…№):
17. Большинство приведенных выше операторов достаточно известны из математического аппарата матричных вычислений. Под необычным для нашей математической литературы является понятие «векторизация», под которой подразумевается одновременное проведение некоторой скалярной операции над всеми элементами вектора или матрицы, полученными оператором векторизации. Это можно понимать и как возможность параллельных вычислений.
Векторизация осуществляется помещением соответствующего выражения под знак длинной стрелки и позволяет использовать скалярные операторы и функции с массивами. Нередко это заметно упрощает запись математических алгоритмов, особенно для обеспечения параллельных вычислений.
Сравните вышеприведенные выражения с использованием и без использования операторов векторизации.
2. Векторные функции
18. Функция, возвращающая число элементов вектора:
19. Функция, возвращающая номер последнего элемента вектора:
20. Функции, возвращающие максимальное и минимальное значение элементов вектора (или матрицы):
21. Функции, возвращающие вектор действительных и мнимых частей вектора с комплексными элементами:
3. Функции, возвращающие специальные характеристики матриц
22. Функция возвращает число столбцов матрицы:
23. Функция возвращает число строк матрицы:
24. Функция возвращает среднее значение элементов массива:
4. Функции сортировки для вектора и матрицы
25. Функция сортировки элементов вектора в порядке возрастания их значений:
26. Функция перестановки строки матрицы таким образом, чтобы отсортированной оказалась n-ая строка:
27. Функция перестановки столбца матрицы таким образом, чтобы отсортированной оказалась n-й столбец:
28. Функция, изменяющая порядок расположения элемента вектора на противоположный (начиная с конца) – реверсирование:
5. Матричные функции
29. Функция, объединяющая в одну две и более матриц имеющие одинаковое число строк по горизонтали:
30. Функция, объединяющая две и более матриц, имеющие одинаковое число столбцов по вертикали:
31. Функция – возвращает субматрицу, состоящую из всех элементов, содержащихся в строках от ir до jr и столбцов с ic до jc (ir < jr и ic < jc):
6. Решение системы линейных уравнений
Если задана система из n линейный уравнений для которой можно сформировать матрицу, составленную из коэффициентов при неизвестных (например, M1) и матрицу-вектор, составленную из свободных членов системы уравнений (например, V1), то согласно правилам высшей математики если определитель |M1|≠0, то решение данной системы из n линейных уравнений можно найти в следующем виде (например, матрацу-вектор F):
Поскольку решение систем из n линейных уравнений довольно распространенная задача, то в MathCAD введена встроенная функция lsolve(A,B), которая возвращает матрицу вектор решения системы из n линейных уравнений при заданной матрице коэффициента и векторе свободных членов:
7. Решение системы нелинейных уравнений
При решении систем нелинейных уравнений в системе MathCAD используется специальный вычислительный блок, открываемый служебным словом — директивой Given — и имеющий следующую структуру:
Начальные условия
Given
Уравнения
Ограничительные условия
Выражения с функциями Find, Minerr, Minimize и Maximize
Начальные условия определяют начальные значения искомых переменных и задаются в виде var:=value, т.е. обычным присваиванием переменным заданных значений. Если переменных несколько, то можно использовать векторное представление для начальных условий. Уравнения задаются в виде expr_left=expr_right с применением жирного знака равенства между левой и правой частями каждого уравнения. Ограничительные условия обычно задаются в виде неравенств или равенств, которые должны удовлетворяться при решении системы уравнений.
8. Приемы построения и форматирования 2D и 3D графиков в системе MathCAD
К двумерным графикам относят графики в декартовой и полярной системах координат. Созданный однажды график одного типа нельзя переделать в график другого типа (в отличие от трехмерных графиков).
Для создания декартового графика необходимо нажать кнопку X-Y Plot на панели Graph и вставить вместо заполнителей по осям X и Y два ряда данных.
Т.к. в дальнейшем при создании математических моделей рычажных механизмов с последующей анимацией (визуализацией) их кинематических схем в основном будут использоваться декартовые графики, то следует более подробно ознакомиться с приемами их форматирования.
Построим на одном декартовом графике три функции одной переменной (см. рисунок 1.4): x·sin(x), 2·x·sin(x), и sin(x), предварительно задавшись следующими пределами изменения переменной x:=-15,-14.5..15.
Для создания полярного графика необходимо нажать кнопку Polar Plot на панели Graph (График) и вставить вместо заполнителей имена переменных и функций, которые будут нарисованы в полярной системе координат: угол (нижний заполнитель) и радиус-вектор (левый заполнитель). Точно так же, как при создании декартова графика, по осям могут быть отложены два вектора, элементы векторов и ранжированные переменные в различных сочетаниях, а также может быть осуществлено быстрое построение графика функции.
Построим на одном графике две полярные функции одной переменной (см. рисунок 1.5): 5·cos(j) и 5·sin(2·j), предварительно задавшись следующими пределами изменения переменной j:=0,0.1·p..2·p.
а) б)
а –график по умолчанию; б –график с настройками пользователя
Рисунок 1.4 – Построение XY-графика
а) б)
а –график по умолчанию; б –график с настройками пользователя
Рисунок 1.5 – Построение полярного графика
На декартовых и полярных графиках есть возможность нанесения дополнительных линий – так называемых маркеров.
Чтобы создать трехмерный график, требуется нажать кнопку с изображением любого из типов трехмерных графиков на панели инструментов Graph (График). В результате появится пустая область графика с тремя осями и единственным заполнителем в нижнем левом углу. В этот заполнитель следует ввести либо имя функции двух переменных для быстрого построения трехмерного графика, либо имя матричной переменной, которая задаст распределение данных на плоскости.
Построим на трехмерном графике распределения данных для одной из заданных матриц, например для матрицы M2 (см. рисунок 1.6).
а) б)
а –график по умолчанию; б –график с настройками пользователя
Рисунок 1.6 – Построение трехмерного графика
ДОПОЛНИТЕЛЬНОЕ ЗАДАНИЕ
1. Построенные по умолчанию в системе MathCAD графики (XY-график, полярный график и трехмерный график) привести в соответствии с рисунками 1.4 б, 1.5 б и 1.6 б.
2. На чистом листе формата А4 провести графическую проверку сложения и вычитания двух векторов V1 и V2, а также замерить модуль результирующего вектора.
3. Сделать выводы по лабораторной работе.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое вектор и матрица?
2. Что такое единичный вектор, нулевой вектор, радиус-вектор?
3. Классификация векторов.
4. Правила сложения и вычитания векторов.
5. Векторное и скалярное произведение двух векторов, их геометрический и физический смысл.
6. Основные свойства скалярного и векторного произведений.
7. Способы задания и выделения элементов векторов и матриц в системе MathCAD.
8. Основные операции с векторами и матрицами в системе MathCAD.
9. Способы создания и форматирования графиков в системе MathCAD.
10. Способы решения систем уравнений в системе MathCAD.
Надеюсь, представленные на сайте материалы окажутся полезными для Вашей научной или практической деятельности и буду признателен за упоминание моих работ в списке Вашей литературы при их использовании.
Данные лабораторные работы были разработаны автором в рамках преподавания курса «Математическое моделирование» на кафедре «Сельскохозяйственные машины» в ГГТУ имени П.О. Сухого в период 2005-2008 гг. для студентов дневной и заочной формы обучения. В данных лабораторных работах максимально учтены все замечания, выявленные в процессе обучения, но сохранена форма изложения материала, для передачи духа того времени.
Ссылка на лабораторную работу №2 в формате *.pdf
Ссылка на карточки защиты лабораторной работы №2 в формате *.pdf












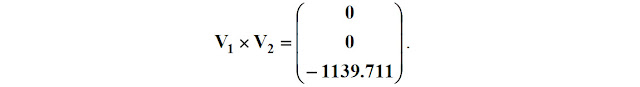








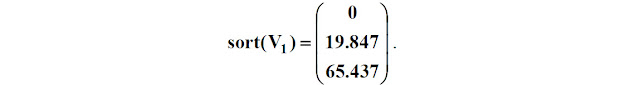












Комментариев нет:
Отправить комментарий