От автора: предлагаемый векторный метод исследования рычажных механизмов, как и любой другой метод аналитического описания, требует соответствующего теоретического обоснования. По мере публикации материалов на станицах данного электронного ресурса, раздел «Аналитические зависимости» будет периодически пополняться различными математическими (функциональными) зависимостями, необходимыми для проведения кинематического, силового и динамического анализа рычажных механизмов. Постепенное расширение этого раздела позволит получить полное и всестороннее понимание предлагаемого метода и его применения на практике, предоставляя ясное и понятное объяснение каждой формулы с соответствующими иллюстрациями и примерами. Цель – дать все необходимые знания для практического применения векторного метода исследования рычажных механизмов в максимально наглядной и доступной форме.
1. Принятые понятия и условные обозначения
Для наглядности и простоты понимания предлагаемого векторного метода исследования рычажных механизмов введем следующие понятия и условные обозначения.
Вектор, обозначенный одной буквой латинского алфавита (например, A), будем называть абсолютным вектором, т.е. координатами точки относительно начала принятой прямоугольной системы координат. Вектор, обозначенный двумя буквами латинского алфавита (например, AB), будем называть относительным вектором, т.е. координатой второй точки относительно первой. Суть обоих введенных понятий абсолютно одинакова т.к. и вектор, называемый абсолютным, и вектор, называемый относительным – это координата одной точки относительно другой.
Длины звеньев рычажного механизма будем обозначать тремя буквами латинского алфавита, где первой буквой всегда будет идти L, а две следующие буквы будут соответствовать обозначению точек рычажного механизма, которые соединяют данное звено (например, LAB).
Углы между звеньями рычажного механизма будем обозначать тремя буквами латинского алфавита, где средняя буква будет соответствовать точке с вершиной в данном угле (например, ABC – угол с вершиной в точке B).
2.1 Аналитические зависимости для описания кинематики точек и звеньев
Основой предложенного векторного метода исследования рычажных механизмов для описания кинематики движения всех характерных точек и звеньев механизма является система аналитического преобразования координат исходного вектора в вектор, который может быть получен из исходного путем поворота его на некоторый угол в заданном направлении в рассматриваемой плоскости (известный как метод преобразования координат или метод векторного преобразования координат).
Пусть исходное звено рычажного механизма представлено в виде относительного вектора OA, а начало правой прямоугольной системы координат расположено в точке O (см. рисунок 1, а). Предположим, что относительный вектор ОА, который составляет угол β с осью X принятой системы координат, необходимо повернуть на некоторый угол α вокруг оси Z против хода часовой стрелки без изменения его длины. В результате такого поворота, получим новый относительный вектор ОВ, который будет составлять угол β+α с осью Х принятой системы координат.
а) б)
Рисунок 1 – Поворот исходного вектора OA вокруг оси Z против хода часовой стрелки
а – без изменения длины LOA=LOB; б – с изменением длины LOA≠LOB
Тогда выражение для нахождения нового относительного вектора OB можно представить в следующем матричном виде:
Выражение (1) означает, что новый относительный вектор OB может быть получен из исходного вектора OA путем его поворота вокруг оси Z на угол α против хода часовой стрелки, если смотреть на острие оси Z. Для этого первый множитель правой части выражения (1), который представляет собой матрицу поворота системы координат исходного вектора, необходимо умножить на исходный относительный вектор OA, который представлен в виде второго множителя. В этом случае полученный новый относительный вектор OB будет иметь длину такую же, как исходный относительный вектор вектор OA, но другое направление в пространстве.
Рассмотрим случай (см. рисунок 1, б), когда при повороте исходного относительного вектора OA на угол α вокруг оси Z против хода часовой стрелки необходимо получить новый относительный вектор OB с длиной отличной от длины исходного относительного вектора OA (LOA≠LOB). В этом случае необходимо полученный с помощью выражения (1) вектор умножить на длину нового вектора LOB и разделить на модуль исходного относительного вектора OA:
Выражение (2) можно назвать универсальным, так как его можно использовать для нахождения нового вектора, как с изменением его длины, так и без изменения длины.
Как известно, современные математические пакеты и языки программирования позволяют достаточно легко формализовать предложенный векторный метод исследования рычажных механизмов, путем использования так называемых функций пользователя. В результате аналитическое описание рычажных механизмов предложенным векторным методом исследования получается более наглядным и компактным.
Так правую часть выражения (2) можно представить в виде следующей функции пользователя, которую будем называть «функцией поворота вектора»:
где V – исходный поворачиваемый вектора; α – угол поворота исходного вектора (значение угла принимается со знаком «+» при осуществлении поворота исходного вектора против хода часовой стрелки (если смотреть на острие вектора Z, а при повороте по ходу часовой стрелки – со знаком «-»); Lnew – длина нового вектора; MXY(α) – матрица направляющих косинусов (в некоторых литературных источниках можно встретить другие названия, такие как матрица поворота или матрица преобразования координат). Нижний индекс XY говорит о том, что поворот исходного вектора осуществляется в плоскости XY вокруг оси Z, а сама матрица направляющих косинусов имеет следующий вид:Вторая форма записи матрицы направляющих косинусов в выражении (4) была получена путем применения к синусам формул приведения. Обе формы записи матрицы направляющих косинусов могут применяться наравне друг с другом, однако вторая форма записи наиболее полно соответствует своему названию. Необходимо обратить внимание, что для второй формулы в выражении (4), все используемые угловые величины имеют размерность градусы для более наглядного представления. В случае необходимости использования угловых величин в радианах, необходимо внести соответствующие изменения для второй формулы в выражении (4).
а) б) в)
Рисунок 2 – Выбор матрицы направляющих косинусов при различных вариантах расположения рычажного механизма на плоскости
а – плоскость XY; б – плоскость YZ; в – плоскость ZX
Стоит отметить, что выражение (4) соответствует случаю, когда анализируемый рычажный механизм лежит в плоскости XY правой прямоугольной системы координат (см. рисунок 2, а), а поворот исходного вектора осуществляется вокруг оси Z. В случае если анализируемый рычажный механизм лежит в плоскости YZ или ZX правой прямоугольной системы координат (см. рисунок 2, б или в), а поворот исходного вектора осуществляется вокруг оси X или Y, то в выражении (4) необходимо использовать соответствующую матрицу направляющих косинусов следующего вида:
Таким образом, используя выражение (3), окончательную форму математической записи преобразования координат исходного относительного вектора OA в новый относительный вектор OB (см. выражение (2)), путем его поворота на некоторый угол в заданном направлении с изменением длины, можно представить в следующем виде (см. рисунок 1, б):
Выражение (6) означает, что вектор OB может быть получен из вектора OA путем его поворота вокруг оси Z на угол α против хода часовой стеки в плоскости XY с изменением его длины на новую длину LOB. Выражение (6) приведено в качестве примера для пояснения математической формы записи преобразования одного относительного вектора в другой, а основным аналитическим выражением для предложенного векторного метода исследования рычажных механизмов через преобразование координат будет всегда оставаться выражение (3).
Для аналитического описания рычажных механизмов предложенным векторным методом понадобится еще несколько дополнительных функций. Так как все рычажные механизмы будут анализироваться в правой прямоугольной декартовой системе координат, то для каждой из ее осей можно задаться соответствующим единичным вектором (ортом) – вектор, модуль которого равен единицы:
В случае необходимости нахождения единичного вектора (орта) любого произвольного вектора, необходимо данный вектор разделить на его длину, что можно представить в виде следующей пользовательской функции:
Используемый в выражении (3) угол α поворота исходного вектора может быть задан как в виде исходных данных или должен быть непосредственно определен в процессе аналитического описания предложенным векторным методом (методом векторного преобразования координат). Определение неизвестных величин углов, на которые необходимо поворачивать исходные относительные вектора для нахождения неизвестных векторов в выражении (3), будем осуществлять по теореме косинусов из треугольника с известной длиной всех сторон с помощью следующей пользовательской функции:
где L1 и L2 – стороны треугольника, прилежащие к искомому углу; L3 – сторона треугольника, противолежащая искомому углу.
Таким образом, с помощью выражений (3), (8) – (9) можно аналитически описать кинематику движения всех характерных точек и звеньев рычажных механизмов предложенным векторным методом исследования рычажных механизмов, что и будет сделано на страницах данного электронного ресурса (см. соответствующие разделы с многочисленными примерами и научными работами).
2.2 Аналитические зависимости для описания кинематики звена «ползун»
Рассмотрим рычажный механизм содержащий звено типа «ползун», кинематическая схема которого приведена на рисунке 3. Особенностью данного звена является то, что оно движется только вдоль заранее заданной траектории (вдоль линии, проходящей через точки W1 и W2, абсолютные вектора которых заранее известны).
Рисунок 3 – Кинематическая схема кривошипно-ползунного механизма
Для аналитического описания кинематики звена ползун будет использоваться одно из свойств векторного произведения, согласно которому если сила F, приложенная к т. А звена (см. рисунок 4), представлена в виде вектора AB, то моментом силы F относительно т. O называется вектор M, определяемый формулой:
а) б)
Рисунок 4 – К графическому описанию свойства векторного произведения
а – условные обозначения векторов; б – проекции векторов на координатные оси
Если в выражении (10) вектор силы будет представлен в виде единичного вектора, то модуль такого векторного произведения есть не что иное, как кратчайшее расстояние (плечо) опущенное из т. О, на вектор F (вектор AB):
Для того чтобы представить искомое плечо в виде вектора, лежащего непосредственно в плоскости анализируемого рычажного механизма, необходимо воспользоваться свойством двойного векторного произведения. Для этого силу F, приложенную к т. А звена (см. рисунок 3), необходимо представить в виде единичного вектора AB (орта), тогда двойное векторное произведение данной силы на радиус-вектор и снова на данную силу даст вектор кратчайшего расстояния от т. О, до данной силы. Данное выражение можно представить в следующем виде:
С учетом описанных выше свойств векторного и двойного векторного произведения, для описания кинематики звена ползун требуется выполнить ряд вспомогательных математических вычислений, которые не несут дополнительной информации. Поэтому наилучшим способом для аналитического нахождения абсолютного вектора точки ползуна, было бы создание отдельной пользовательской функции, внутри которой происходили бы все необходимые дополнительные математические вычисления. Современные математические пакеты и языки программирования позволяют создавать отдельные блоки таких процедур или функций, на вход которых подаются необходимые исходные данные, на основании которых внутри процедуры или функции производится все математические операции, а на выходе выдается интересующий результат.
Так нахождение абсолютного вектора точки ползуна можно представить в виде некоторой пользовательской функции, к которой можно будет обращаться, исключая промежуточные операции. Данную пользовательскую функцию можно представить в следующем виде:
где A – вектор-точка начала шатуна (вектор-точка окончания кривошипа); LAB – длина шатуна; W1 – первая вектор-точка направляющей движения ползуна; W2 – вторая вектор-точка направляющей движения ползуна; W – вектор-точка одной из направляющих движения ползуна, характеризующая одно из конструктивных положений ползуна, т.е. одно из двух возможных вариантов сборки механизма.
Используя выражение (13) аналитическую запись нахождения некоторого абсолютного вектора точки ползуна B(j), приведенного на рисунке 3, можно записать в следующем виде:
В вышеприведенном выражении в качестве последней переменной функции ползуна используется координата точки W1 направляющей, что соответствует расчетной схеме сборки рассматриваемого рычажного механизма. Полученная функция пользователя нахождения точки ползуна получилась достаточно компактной и наглядной. Дополнительную информацию по описанию алгоритма нахождения абсолютного вектора точки ползуна можно ознакомиться в работе: Котов А.В. Анализ уравновешенности кривошипно-ползунного механизма привода режущего аппарата методом векторов главных точек
3. Аналитические зависимости для нахождения скоростей и ускорений
При кинематическом анализе механизмов скорости и ускорения звеньев и точек, им принадлежащих, удобно выражать в функции угла поворота или перемещения начального звена или определять так называемые аналоги. Такой путь решения позволяет задачу о кинематическом исследовании свести к задаче определения некоторых геометрических характеристик схемы, используя которые при заданном законе изменения по времени обобщенных координат механизма, можно определить действительные скорость и ускорение:
Если известен вектор, который описывает абсолютную (относительную) координату некоторой точки или звена рычажного механизма, то, взяв от этого вектора первую производную по обобщенной координате (углу или перемещению) можно определить аналоги абсолютной (относительной) скорости этой точки или звена (первую передаточную функцию):
Если известен вектор, который описывает абсолютную (относительную) координату некоторой точки или звена рычажного механизма, то, взяв от этого вектора вторую производную по обобщенной координате (углу или перемещению) можно определить аналоги абсолютной (относительной) ускорения этой точки или звена (вторую передаточную функцию):
Если известен вектор, который описывает относительную координату некоторого звена рычажного механизма, а также известен аналоги скорости данного звена, то для определения аналога угловой скорости некоторого звена, необходимо вектора этого звена умножить векторно на аналог скорости звена, а результирующий вектор разделить на модуль вектора звена:
По аналогии с выражением (16) можно найти аналог углового ускорения звена, только в этом случае в данном выражении вместо аналога ускорения используется аналог скорости, а остальные параметры остаются без изменения:
Как видно, приведенные выражения легко поддаются формализации в современных математических пакетах и языках программирования. Например, в математическом пакете MathCAD вышеприведенные выражения для нахождения скоростей и ускорений точек или звеньев механизма можно представить как:
Как видно из выражений (14) – (17) при вычислении аналогов скоростей и ускорений (линейных и угловых) в выражениях меняется лишь обобщенная координата, поэтому данные выражения можно считать универсальными вне зависимости от выбора той или иной обобщенной координаты.
4. Аналитические зависимости для силового анализа
{... материал готовится к размещению}
5. Аналитические зависимости для пространственных механизмов
{... материал готовится к размещению}
Надеюсь, представленные на сайте материалы окажутся полезными для Вашей научной или практической деятельности и буду признателен за упоминание моих работ в списке Вашей литературы при их использовании.







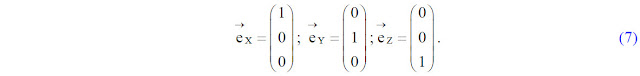









Комментариев нет:
Отправить комментарий