Авторы: Бобыренко С.Н. Котов А.В.
В работе, на основе теоретических методов, выполнен анализ технологического процесса работы питающего аппарата кормоуборочного комбайна. Дана методика и порядок расчета функциональной математической модели механизма подпрессовки питающего аппарата, учитывающая зависимость толщины слоя растительной массы между различными парами вальцев от физико-механических параметров убираемой культуры. Основы разработанного авторами алгоритма используются в РКУП «ГСКБ по зерноуборочной и кормоуборочной технике» для автоматизированного проектирования вальцевых питающих аппаратов
Введение
Состояние и уровень развития животноводства находятся в непосредственной зависимости от объема и качества заготавливаемых кормов. Прочной кормовой базе необходимы современные высокопроизводительные кормоуборочные комбайны и передовые технологии заготовки кормов.
Известно, что при выполнении кормоуборочным комбайном технологического процесса до 80% затрат мощности приходится на измельчающий аппарат. Энергоемкость процесса резания напрямую зависит от двух главных факторов: конструктивных особенностей режущей пары и состояния поступающей в зону резания растительной массы. В свою очередь последний фактор определяется параметрами механизма подпрессовки питающего аппарата: чем выше уплотнение поступающей на измельчение растительной масса и меньше толщина перерезаемого слоя, тем менее энергоемок процесс резания [1].
В настоящее время конструкторами, при выборе рациональных параметров элементов питающего аппарата используется только их собственные знания и опыт, а доводка работоспособной конструкции, обеспечивающей заданные параметры производительности, происходит в полевых условиях.
Поэтому разработка методики и порядка расчета математической модели механизма подпрессовки питающего аппарата, учитывающей зависимость толщины слоя растительной массы между различными парами вальцев от физико-механических параметров убираемой культуры, является одной из важных задач по повышению производительности кормоуборочного комбайна.
Описание механизма подпрессовки вальцев
Питающие аппараты всех современных кормоуборочных комбайнов состоят из нескольких вальцев, которые уплотняют слой растительной массы, подаваемый от адаптера к измельчающему аппарату. Все питающие аппараты имеют подвижные верхние и неподвижные нижние вальцы, вращающиеся навстречу друг другу. Число вальцев питающего аппарата варьируется от четырех до шести. Верхние вальцы через рычажно-пружинный механизм – механизм подпрессовки вальцев – прижимаются к нижним, обеспечивая тем самым требуемое уплотнение и толщину растительной массы поступающей в измельчающий аппарат.
В общем случае механизм подпрессовки четырех вальцевого питающего аппарата (рис. 1) состоит из рычага ОА, соединяющего задний верхний валец 4 с рамой питающего аппарата, и рычага АВ, соединяющего верхние подвижные вальцы 2 и 4. Подпрессовывающие пружины 5 (по две с каждой стороны) имеют неподвижные точки крепления на раме питающего аппарата и подвижные на рычаге AB.

Рис. 1 – Схема механизма подпрессовки вальцев питающего аппарата
1, 3 – вальцы нижние; 2, 4 – вальцы верхние; 5 – пружины
Технологический процесс работы механизма подпрессовки вальцев питающего аппарата протекает следующим образом. При подаче в питающей аппарат растительной массы верхние вальцы 2 и 4 перемещаются вверх, а рычаги OA и AB занимают новое положение ОА1 и А1В1, растягивая пружины 5. Валец 4 перемещается по дуге с радиусом ОА, в то время как валец 2 перемещается по дуге радиусом АВ, с центром в точке А.
Точка В, а соответственно и передний валец 2, совершает плоско параллельное движение по сложной траектории относительно рамы питающего аппарата, так как ее положение определяется не только положением центра вращения (точки А), но и высотой поступающего слоя растительной массы, который может варьироваться от наибольшей (валец поднят максимально вверх) до наименьшей величины (минимальный зазор между верхними и нижними вальцами). Крайние положения верхних вальцев ограничены упорами, которые могут иметь различное конструктивное исполнение в зависимости от модели кормоуборочного комбайна.
Исходя из функциональных особенностей технологического процесса питающего аппарата, сформулируем следующие основные требования, предъявляемые к механизму подпрессовки вальцев:
- обеспечение устойчивого приема слоя растительной массы от адаптера, даже при большой неравномерности подачи, и надежной транспортировки к измельчающему аппарату;
- обеспечение уплотнения слоя растительной массы до требуемых параметров;
- обеспечение минимальной энергоемкости выполнения технологического процесса.
Структурный анализ механизма
Геометрическая модель механизма подпрессовки вальцев питающего аппарата представляет собой пространственный шарнирный механизм, симметричный относительно своей продольной плоскости симметрии. Проецируя характерные точки механизма подпрессовки на продольную плоскость симметрии, получаем плоский аналог пространственного механизма с двумя степенями свободы (рис. 2).

Рис. 2 – Кинематическая схема механизма подпрессовки вальцев
Согласно четырехкомпонентной модели Кельвина-Фойгта [2], слой поступающей в питающий аппарат растительной массы, определяющий зазор между передними и задними вальцами, является упруговязким телом, для которого кинематическим аналогом может служить гидроцилиндр (см. рис. 2). Следует отметить, что геометрически точка J крепления условного гидроцилиндра и точка A крепления рычага качания заднего вальца совпадают на плоском аналоге механизма, однако в действительности они являются разнесенными в пространстве.
Наличие двух степеней свободы механизма подпрессовки связано с дополнительной подвижностью заднего вальца, т.е. с возможностью изменения зазора СВ между передними вальцами без изменения зазора DJ между задними вальцами и наоборот, что говорит о статической неопределимости механизма (зависимость всех параметров механизма от нескольких входных данных).
Классический процесс описания математической модели механизма подпрессовки вальцев с двумя обобщенными координатами достаточно сложен и трудоемок и не позволяет учесть зависимость толщины слоя растительной массы между вальцами от физико-механических параметров убираемой культуры.
Поэтому решение задачи статической неопределимости механизма подпрессовки вальцев позволит существенно упростить процесс формирования математической модели за счет использования только одной обобщенной координаты вместо двух.
Раскрытие статической неопределимости
Известно, что в процессе уплотнения растительной массы в питающем аппарате толщина слоя растительной массы между задними вальцами находится в зависимости от следующих параметров:
1. величины зазора между передними вальцами;
2. физико-механических свойств растительной массы (коэффициент релаксации, модуль упругости и т.д.);
3. силовых параметров пружин механизма подпрессовки вальцев;
4. кинематических параметров механизма подпрессовки вальцев.
Согласно технологическому процессу работы питающего аппарата в момент контакта с вальцами слой растительной массы начинает уплотняться от начальной толщины HН до значения межвальцевого зазора Δ. После прохождения зоны максимального нагружения (линии соединяющей центры вальцев) толщина слоя начинает постепенно восстанавливаться до величины H1.
Согласно исследованиям [3, 4] толщина слоя растительной массы между вальцами определяется как:

где F – усилие сжатия пружины; Δ0 – первоначальный зазор между вальцами; Р0 – вес верхнего вальца; b – ширина вальца; D1, D2 – параметры, зависящие от обрабатываемой культуры; НН – толщина слоя массы в момент контакта с вальцами; f – коэффициент трения растительной массы по материалу вальца; ω – угловая скорость вращения верхнего вальца; R – радиус верхнего вальца.
Так как все современные питающие аппараты имеют ребристые или бичевые поверхности, то можно принять допущение о том, что f = 1, в этом случае выражение (1) примет следующий вид:

Параметры D1 и D2 отражают влияние физико-механических параметров культуры, из которой состоит слой растительной массы, на формирование толщины слоя и, соответственно, межвальцевого зазора, определяются следующими выражениями:

где E0, E – соответственно, мгновенный и длительный модули упругости растительной массы; λ0, λ – модули вязкости, определяющие протекание процессов релаксации и ползучести при деформации растительной массы.
Параметры E0, E, λ0, λ в выражениях (3) и (4) изменяются в зависимости от влажности, периода вегетации и др. свойств растительной массы, а также от степени воздействия со стороны вальцев и поэтому могут быть определены только экспериментальным путем.
Толщину слоя на выходе из вальца можно найти как:
где t1 – время начала отрыва слоя растительной массы от вальца; Di – диаметр верхнего вальца.
В выражении (5) время отрыва слоя растительной массы отсчитывается начиная с момента релаксации, т.е. после прохождения зоны максимального нагружения усилием подпрессовки. Учитывая высокие линейные скорости движения растительной массы в питающем аппарате (до 4 м/с), время t1 численно выражается в сотых долях секунды и им можно пренебречь, соответственно выражение (5) можно представить в виде:
Тогда, учитывая зависимости (2) – (6), толщина слоя растительной массы между передними вальцами будет определяться как:
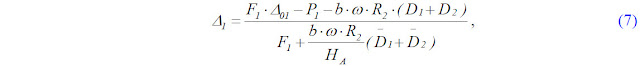
где НА – толщина слоя растительной массы поступающей от адаптера; F1 – усилие подпрессовки на переднем вальце; P1 – вес верхнего переднего вальца; Δ01 – зазор между передними вальцами в момент подачи слоя растительной массы НА.
Толщина слоя растительной массы между задними вальцами будет определяться как:

где F2 – усилие подпрессовки на заднем вальце; P2 – вес заднего вальца; Δ02 – зазор между задними вальцами в момент подачи слоя растительной массы Н1.
Движение слоя растительной массы в питающем аппарате предполагает разницу во времени ТΔ между образованием зазоров между передними (Δ1) и задними (Δ2) вальцами и составляет:
где S – расстояние между осями, соединяющими центры вальцевых пар.
Выражения (7) – (9), позволяют решить проблему статической неопределимости механизма подпрессовки питающего аппарата, так как явно показывают зависимость показателей толщины слоя растительной массы в различные моменты времени между передними и задними вальцами, а так же учитывают физико-механические свойства убираемой культуры:
где VКК – скорость движения кормоуборочного комбайна; NA – внутренние параметры адаптера (ширина захвата, размеры выгрузного окна и т.п.); Q – физико-биологические параметры убираемой культуры.
Таким образом, согласно выражению (10) при разработке математической модели механизма подпрессовки вальцев питающего аппарата в качестве обобщенной координаты можно использовать как показатель НА (при исследовании работы питающего аппарата в связке с конкретным адаптером), так и показатель Δ1 (в случае проверки параметров механизма подпрессовки с убираемой культурой).
Аналитические зависимости
В данной работе представлен векторный метод исследования рычажных механизмов, основанный на методе преобразования координат, который уже более 10 лет успешно применяется в РКУП «ГСКБ по зерноуборочной и кормоуборочной технике» при проектировании рычажных механизмов сельскохозяйственных агрегатов [5]. Этот метод отличается простотой и наглядностью, легко поддается формализации и алгоритмизации в любых современных математических пакетах и языках программирования.
При описании векторного метода введены следующие понятия. Вектор, обозначенный одной буквой, будем называть абсолютным вектором, т.е. координатами точки относительно начала принятой системы координат. Вектор, обозначенный двумя буквами, будем называть относительным вектором, т.е. координатой второй точки относительно первой. Суть обоих введенных понятий абсолютно одинакова т.к. и вектор называемый абсолютным, и вектор называемый относительным – это координата одной точки относительно другой. Эти понятия введены дополнительно для наглядности и простоты понимания приведенного в работе математического описания.
Основой рассматриваемого векторного метода исследования рычажных механизмов является система аналитического преобразования координат исходного вектора в вектор, который может быть получен из исходного путем поворота его на некоторый угол в заданном направлении в рассматриваемой плоскости:

где V – поворачиваемый вектор; α – угол поворота исходного вектора. Причем значение угла α принимается со знаком «+» при осуществлении поворота исходного вектора против часовой стрелки, а при повороте по часовой стрелки – со знаком «-».
Выражение (11) означает, что вектор V1 может быть получен из вектора V путем его поворота на угол α в рассматриваемой плоскости. Для чего первый множитель правой части выражения (11), который представляет собой матрицу направляющих косинусов поворота, необходимо умножить на исходный вектор, который представлен в виде второго множителя. В этом случае полученный вектор будет иметь длину такую же, как исходный вектор, но другое направление.
Для получения повернутого в плоскости вектора, имеющего заданную, не равную исходному поворачиваемому вектору, длину необходимо полученный с помощью выражения (11) вектор умножить на его длину и разделить на модуль исходного вектора. Это преобразование можно записать в виде выражения (12):

где Lnew – длина нового вектора.
Определение величин углов, на которые необходимо поворачивать известные вектора для нахождения неизвестных векторов, будем осуществлять по теореме косинусов для треугольника с известной длиной всех сторон:

где L1 и L2 – стороны треугольника, прилежащие к искомому углу; L3 – сторона треугольника, противолежащая искомому углу.
Геометрический анализ
Аналитическое описание механизма подпрессовки питающего аппарата кормоуборочного комбайна с учетом выражений (11) – (13) представим в следующем виде.
Диапазон изменения обобщенных координат осуществляется в следующих пределах:
где Zпер и Zзад – текущий зазор между передними и задними вальцами соответственно; Δ1 и Δ2 – приращение изменения зазора между передними и задними вальцами соответственно.
Учитывая зависимости (10), полученные ранее, величину зазора между задними вальцами запишем в следующем виде:
![]()
Определим межосевое расстояние между передними и задними вальцами:

Положение всех характерных точке механизма подпрессовки вальцев можно описать с помощью формул (18) – (33).
Найдем угол ODJ(Zпер,TΔ) между векторами DO и DJ(Zпер,TΔ) при вершине в точке D треугольника ODJ:
где |DO| – модуль вектора DO, определяющий длину между двумя векторами D и O; LDJ(Zпер,TΔ) и LOJ – длины звеньев механизма подпрессовки.
Выражением (20) получаем относительный вектор DJ(Zпер,TΔ) путем поворота вектора DO на угол ODJ(Zпер,TΔ) против часовой стрелки с изменением его длины на рассчитанную длину LDJ(Zпер,TΔ).

Так как положение всех характерных точек механизма подпрессовки вальцев питающего аппарата для любого положения определено, длина подпрессовывающих пружин в процессе работы механизма определяется из выражений:
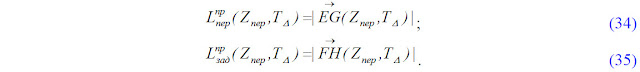
Как известно, в конструкциях верхних вальцев современных питающих аппаратов кормоуборочных комбайнов диаметр переднего вальца значительно превышает диаметр заднего вальца, а максимальный зазор между передними вальцами соизмерим или превышает диаметр заднего вальца. Такая особенность конструкции питающего аппарата может привести к остановке технологического процесса подачи растительной массы к измельчающему аппарату, когда верхняя часть слоя растительной массы подается выше оси вращения заднего верхнего вальца. В этом случае бичи заднего вальца, встречаясь с верхней частью слоя растительной массы, начинают отталкивать ее назад, что ведет к скоплению растительной массы, протягиванию ее между верхними вальцами и наматыванию на них. В результате срабатывания предохранительного устройства происходит полная остановка питающего аппарата.
Исходя из вышесказанного, сформулируем «условие незаклинивания вальцев», определяемое геометрическим положением передних и задних вальцев относительно друг друга:
где α1 – угол наклона межосевой линии СВ передних вальцев к вертикальной оси; α2 – угол наклона межосевой линии DJ передних вальцев к вертикальной оси; D4 – диаметр заднего верхнего вальца.
С учетом вышеприведенных математических зависимостей, преобразуем условие (36) к следующему виду:

Необходимо отметить, что в выражении (37) величина начального зазора Δ02 является текущей величиной зазора между задними вальцами, соответствующей зазору Δ1 между передними вальцами.
Таким образом, выражениями (14) – (35) описывается кинематика всей рассматриваемой системы в целом, а сформированная авторами математическая модель позволяет связать воедино как кинематические параметры механизма подпрессовки вальцев питающего аппарата кормоуборочного комбайна, так и физико-механические параметры убираемой растительной массы.
Сформулированное и аналитически описанное выражением (37) «условие незаклинивания вальцев» позволяет заранее устранить «мертвые положения» механизма подпрессовки вальцев, которые могут вызвать остановку технологического процесса, а, следовательно, и снизить нагрузку на элементы привода питающего аппарата.
Заключение
Представленный в работе векторный метод исследования рычажных механизмов позволяет просто и наглядно описывать существующие и проектируемые механизмы подпрессовки вальцев питающих аппаратов кормоуборочных комбайнов с учетом физико-механических параметров убираемой растительной массы.
Этот метод легко поддается формализации и алгоритмизации в любых современных математических пакетах и языках программирования и позволяет применять различные методы оптимизации для решения поставленной технической задачи.
Результаты анализа и разработанная авторами методика были приняты к реализации в РКУП «ГСКБ по зерноуборочной и кормоуборочной технике» при модернизации кормоуборочного комплекса КВК-800 «Палессе FS80» и разработке питающего аппарата кормоуборочного комплекса КВК-8060 «Палессе FS8060».
Список литературы
1. Резник, Н.Е. Теория резания лезвием и основы расчета режущих аппаратов / Н.Е. Резник. – М.: «Машиностроение», 1975. – 311 с.
2. Оренштейн, В.Е. Рабочий процесс питающе-измельчающего аппарата кормоуборочного комбайна: автореф. дис. на соиск. уч. степ. канд. техн. наук / В.Е. Оренштейн; – РИСХМ. – Ростов-н/Д., 1987. – 24 с.
3. Исследование измельчающего аппарата кормоуборочного комбайна КСК-100 с целью с целью изыскания параметров, обеспечивающих снижение на 5-10% процесса измельчения и обеспечения стабильного качества измельчения: Отчет о НИР (промежуточный) / Рук. А.Г. Карапетьян; – РИСХМ. – Ростов-н/Д., 1985. – 105 с.
4. Калина, А.А. Система динамической защиты приводов рабочих органов кормоуборочных комбайнов: дис. на соиск. уч. степ. канд. техн. наук / А.А. Калина; – БНТУ. – Мн., 2004. – 148 с.
5. Котов, А.В. Применение векторного анализа для оптимизации механизма привода системы очистки зерна зерноуборочного комбайна при его проектировании / А.В. Котов, Ю.В. Чупрынин // Механика машин, механизмов и материалов. – 2009. № 2(7). – С.43-48.
Любое цитирование текста, использование тезисов или иллюстраций из данной статьи допускается только с указанием обязательной ссылки на первоисточник. Пожалуйста, уважайте авторские права и интеллектуальную собственность.
Для цитирования данной работы | To cite this work:
Бобыренко, С. Н. Моделирование процесса работы механизма подпрессовки питающего аппарата кормоуборочного комбайна / С. Н. Бобыренко, А. В. Котов // Вестник Белорусско-Российского университета. – 2011. – №1(30). – С. 18-26. – DOI: https://doi.org/10.53078/20778481_2011_1_18. – EDN NWBXWX.
Babyrenka S. N., Kotov A. V. Modelirovaniye protsessa raboty mekhanizma podpressovki pitayushchego apparata kormouborochnogo kombayna [The simulation of the operation of pre-pressing mechanism of the feed unit of the fodder harvester]. Vestnik Belorussko-Rossiyskogo universiteta [Belarusian-Russian University Bulletin]. Mogilev, 2011, vol. 30, no. 1, pp. 18-26 (in Russ.). DOI: https://doi.org/10.53078/20778481_2011_1_18.
Комментариев нет:
Отправить комментарий