Авторы: Котов А.В.
ЦЕЛЬ РАБОТЫ
1. сформировать математическую модель механизма уравновешивания адаптера с помощью предложенного векторного метода исследования, включающую геометрический, кинематический и силовой анализ; 2. провести визуализацию механизма уравновешивания с адаптером; 3. обеспечить с помощью метода мгновенных мощностей уравновешивание адаптера; 4. провести расчет основных характеристик уравновешивающей пружины растяжения.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Основное назначение механизма уравновешивания состоит в обеспечении процесса копирования рельефа поля адаптером, как в продольном, так и в поперечном направлениях, а также поддержания максимально возможного постоянства давления на почву опорных башмаков адаптера в рекомендуемых пределах.
Данные типы механизмов по способу уравновешивания массы адаптера можно условно разделить на три основные группы: рычажно-пружинные, гидравлические и смешанные. Наибольшее распространение в отечественной практике сельскохозяйственного машиностроения получили рычажно-пружинные типы механизмов уравновешивания адаптеров. В данных механизмах копирование рельефа поля адаптером и регулировка давления его опорных башмаков на почву обеспечивается соответствующей настройкой уравновешивающих пружин совместно с регулировкой звеньев рычажного механизма. В результате настройки происходит частичное снятие нагрузки с опорных башмаков адаптера и переноса ее на уравновешивающие пружины механизма.
Типовая схема механизма уравновешивания адаптера для двух вариантов его настройки приведена на рисунке 5.1.

а) б)
а – настройка на ближнюю точку крепления регулировочной тяги механизма;
б – настройка на дальнюю точку крепления регулировочной тяги механизма;
Рисунок 5.1 – Типовая схема механизма уравновешивания адаптера
Как правило, механизм уравновешивания должен гарантированно обеспечить копирование рельефа поля адаптером в пределах ±100 мм от линии условного горизонта. При этом рекомендуемое давление на почву копирующих башмаков адаптера должно находиться в пределах 300…500 Н (40 ± 10 кг). При повышенном давлении опорные башмаки адаптера быстро изнашиваются и вызывают эрозию почвы, а при пониженном – ухудшается копирование рельефа поля.
Обычно уравновешивающие пружины расположены с двух сторон относительно продольной плоскости симметрии механизма уравновешивания адаптера, образуя с каждой его стороны так называемые пружинные блоки, каждый из которых может содержать от двух и более пружин (см. рисунок 5.1).
Фиксация уравновешивающих пружин в точках их крепления осуществляется через пружинные зацепы, имеющие различное конструктивное исполнение. На рисунке 5.2 приведена схема уравновешивающей пружины растяжения, у которой в роли зацепов используются пружинные пробки и регулировочные болты.
В связи с использованием пружинных пробок, пружина уравновешивания имеет дополнительные нерабочие витки не участвующие в процессе деформации, а служащие только для фиксации на пружинных пробках (обычно не менее трех витков с каждой стороны пружины). В таком случае в технической характеристике на пружину указывается ее полное число витков (n1) и число рабочих витков (n).

1 – уравновешивающая пружина растяжения; 2 – пружинная пробка; 3 – регулировочный болт
Рисунок 5.2 – Схема уравновешивающей пружины растяжения
На рисунке 5.2 приведены также условные обозначения основных параметров пружины растяжения – диаметра проволоки (d); внутреннего диаметра (D1); длины пружины в свободном состоянии (L0); суммарной длины зацепов пружины (Lzac=Lzac1+Lzac2); силы на пружине при предварительной (S1), рабочей (S2) и максимальной (S3) деформации соответственно. Как известно, пружина – деталь машины или механизма для поглощения, накопления и отдачи механической энергии при своем деформировании. Поэтому при выборе уравновешивающих пружин в первом приближении руководствуются величиной накопленной пружиной потенциальной энергией, которую сравнивают с энергией потребной для подъема-опускания адаптера в процессе копирования рельефа поля.
Потребная потенциальная энергия для подъема-опускания адаптера в процессе копирования рельефа поля равна разности между потенциальными энергиями изменения высоты подъема центра тяжести уравновешиваемого адаптера и точки контакта башмака с опорной поверхностью:
Накопленную потенциальную энергию пружины (с рекомендуемым из опыта эксплуатации сельскохозяйственных машин в РКУП «ГСКБ по зерноуборочной и кормоуборочной технике» запасом по максимальной силе) можно определить по следующему выражению:

где s3 – максимальная деформация одного витка пружины, м; c1 – жесткость одного витка пружины, Н/м; kpr – количество пружин, шт; n – число рабочих витков пружины.
Если условие E2>E1 выполняется, то в первом приближении выбор параметров уравновешивающей пружины прекращается.
После проверки выбранных параметров уравновешивающей пружины по потенциальной энергии необходимо определить потребную силовую характеристику пружины, обеспечивающей рекомендуемую величину реакции на башмаках адаптера. С этой целью проводится силовой анализ механизма уравновешивания одним из следующих способов: 1. графическим; 2. составлением уравнения моментов в векторном виде; 3. методом мгновенных мощностей; 4. позвенным анализом. Каждый из приведенных способов имеет свои достоинства и недостатки, а также наиболее рациональную область применения.
В данной лабораторной работе будет рассмотрен силовой анализ механизма с использованием метода мгновенных мощностей. Сущность данного метода заключается в следующем: если известны все вектора внешних сил и известны аналоги скоростей точек или звеньев приложения этих сил, то сумма скалярных произведений векторов внешних сил на аналоги скоростей точек или звеньев их приложения должна равняться нулю:
Левая часть выражения (5.3) представляет собой сумму проекций всех внешних сил на направление скоростей точек или звеньев их приложения, умноженных на величины аналога этой скорости, что согласно физике, представляет собой мощность. Отсюда и название данного метода – метод мгновенных мощностей.
Метод мгновенных мощностей может используется для нахождения только одной неизвестной внешней силы, направление действия которой заранее известно. Данный метод довольно прост в применении и в сложных механизмах часто бывает единственно приемлемым.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Исходные данные
Кинематическая схема механизма уравновешивания с адаптером приведена на рисунке 5.3. Начало системы координат расположено в точке P0 и проходит через ось качания адаптера – точку P1, линию условного горизонта и продольную ось симметрии механизма уравновешивания адаптера: ось X направлена по ходу движения энергосредства; ось Y направлена вертикально вверх; ось Z направлена на наблюдателя (вправо по ходу движения энергосредства). Адаптер с центром тяжести в точке P10 имеет опорные башмаки в точке P9.

Рисунок 5.3 – Кинематическая схема механизма уравновешивания адаптера
Координаты всех неподвижных точек механизма уравновешивания непосредственно привязаны к координатам точки качания адаптера P1 и соответственно равны, м:

Длины звеньев механизма, м:
– с фиксированной длиной
– с настраиваемой длиной (регулировочная тяга)
Углы наклона звеньев, град:
Параметры адаптера:
– длины звеньев, м
– углы между звеньями, град
– масса, Н
– число опорных башмаков, шт
Для большинства адаптеров, спроектированных в РКУП «ГСКБ по зерноуборочной и кормоуборочной технике», величину нагрузки, приходящейся на один башмак адаптера в диапазоне копирования рельефа поля ±100 мм рекомендуется устанавливать порядка 40 кг с возможным разбросом нагрузки в пределах 50…60%. Причем, при положении адаптера на условном горизонте величина реакции 40 кг на одном башмаке адаптера является обязательной. В любом случае давление на почву под башмаком не должно превышать »0,1 кг/см2.
Задаемся допустимой реакцией на одном башмаке уравновешиваемого адаптера на условном горизонте, Н:
Геометрический анализ
В качестве обобщенной координаты будет выступать угол наклона стойки адаптера в процессе копирования рельефа поля, который обозначим через j. Пределы изменения данного угла (обобщенной координаты) в диапазоне копирования рельефа поля адаптером ±100 мм будут определены и заданы позже.
Проведем с помощью выражений (5.4)-(5.18) геометрический анализ механизма уравновешивания адаптера предложенным векторным методом исследования рычажных механизмов в зависимости от изменения обобщенной координаты j, т.е. определим положение всех его характерных точек (см. рисунок 5.3):

Положение центра тяжести адаптера можно найти с помощью выражений (5.14) и (5.15):

Положение опорных башмаков адаптера можно найти с помощью выражений (5.16) и (5.17):

Определившись с положением характерных точек механизма уравновешивания адаптера, можно найти полную длину блока пружин между зацепами в процессе работы механизма с адаптером по выражению (5.18):
Теперь найдем пределы изменения обобщенной координаты j (угла наклона стойки адаптера), а именно: минимальное (jmin) и максимальное (jmax) значения, которые определяются вертикальным положением точки контакта башмаков адаптера с опорной поверхностью P9(j)Y в диапазоне копирования рельефа поля ±100 мм. Кроме того найдем величину угла наклона стойки адаптера (обобщенной координаты) при положении адаптера на условном горизонте (jgor). Для нахождения данных параметров необходимо решить с помощью встроенного в систему MathCAD оператора Given систему линейных уравнений (5.19):

Определившись с пределами изменения обобщенной координаты в диапазоне копирования рельефа поля адаптером, выведем результаты геометрического анализа для 11 положений механизма, для чего вводим вспомогательную переменную Npol:=11. Тогда шаг изменения обобщенной координаты для рассчитываемых положений можно найти с помощью выражения (5.20):

Задаемся пределами изменения обобщенной координаты согласно выражению (5.21):
Теперь выведем покоординатно в зависимости от угла наклона стойки адаптера (обобщенной координаты) положение двух найденных характерных точек механизма уравновешивания с адаптером – P9(j) и P10(j) , а также полную длину пружинного блока между точками крепления, которые сводим в таблицу 5.1. Таблица 5.1 также дополнена выводимыми величинами для положения адаптера на условном горизонте, когда угол наклона стойки адаптера (обобщенная координата) равен jgor.
Таблица 5.1 – Результаты геометрического анализа механизма уравновешивания адаптера

На рисунке 5.4 представлена визуализация (анимация) в системе MathCAD смоделированного механизма уравновешивания с адаптером для трех положений механизма: при максимальном (jmax) и минимальном (jmin) угле наклона стойки адаптера, а также при угле наклона стойки для положения адаптера на условном горизонте (jgor).

Рисунок 5.4 – Визуализация (анимация) механизма уравновешивания с адаптером в системе MathCAD
Кинематический анализ
Найдем передаточные отношения всех точек (звеньев) приложения внешних векторов-сил по выражениям (5.22)-(5.24) для последующего их использования в силовом анализе методом мгновенных мощностей:
– передаточное отношение изменения положения точки центра тяжести адаптера
– передаточное отношение изменения положения точки контакта башмаков адаптера с опорной поверхностью
– передаточное отношение изменения длины блока пружин между точками крепления
Выбор пружины растяжения
Параметры пружины растяжения механизма уравновешивания адаптера соответствуют ГОСТ 13772-86 и принимаются согласно таблице 5.2 по номеру варианта студента.
Таблица 5.2 – Параметры пружин по ГОСТ 13772-86

Согласно рассчитываемому в лабораторной работе варианту из таблицы 5.2 задаемся следующими параметрами уравновешивающей пружины:
F3:=10000 Н сила пружины при максимальной деформации;
d:=0,012 м диаметр проволоки;
D1:=0,06 м наружный диаметр пружины;
с1:=1838000 Н/м жесткость одного витка;
s3:=0,005442 м максимальная деформация одного витка.
Считаем, что для рассматриваемого механизма уравновешивания адаптера, симметричного относительной своей продольной оси симметрии, число пружин в пружинном блоке для левой и правой стороны одинаково. В первом приближении задаемся следующим общим числом уравновешивающих пружин и числом рабочих витков пружины:
Силовой анализ
Силовой анализ механизма уравновешивания адаптера проводится методом мгновенных мощностей с целью определения действительной реакции на одном башмаке адаптера в процессе копирования рельефа поля. Для этого согласно выражению (5.3) составим в общем виде уравнение равновесия системы методом мгновенных мощностей:
где vFpr(j) – вектор-сила усилия возникающая в пружине (неизвестная величина); vGadap – вектор-сила веса адаптера (известная величина); vR(j) – вектор-сила реакции на одном башмаке адаптера в процессе копирования рельефа поля (неизвестная величина).
В выражении (5.26) входят две неизвестные величины (vFpr(j) и vR(j)), но согласно приведенным выше теоретическим сведениям метод мгновенных мощностей может использоваться только для нахождения одной неизвестной силы, направление которой заранее известно. Исключим одну из неизвестных сил, применив выражение (5.26) для величины угла наклона стойки (обобщенной координаты) при положении адаптера на условном горизонте (j=jgor) и перепишем выражение (5.26) в следующем виде:

где vFpr_gor – вектор-сила потребного усилия возникающего в пружине при положении адаптера на условном горизонте (неизвестная величина); vRdop – вектор-сила реакции на одном башмаке адаптера при положении на условном горизонте (известная величина).
Представим каждую вектор-силу, входящую в выражение (5.27) как произведение соответствующего единичного вектора на его длину:

После подстановки в выражение (5.27) выражений (5.28)-(5.30) получим:
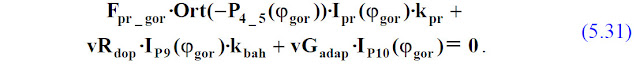
Из выражения (5.31) можно легко выразить неизвестное усилие на одной пружине (скалярную величину) механизма уравновешивания при положении адаптера на условном горизонте:

Для определения силы на уравновешивающей пружине в процессе копирования рельефа поля адаптером в пределах ±100 мм проведем расчет некоторых ее параметров.
Жесткость одной уравновешивающей пружины равна:
Деформация пружинного блока при положении адаптера на условном горизонте:

Начальная длина пружины без учета зацепов:
Потребная начальная длина пружины с учетом длины нерабочей части (зацепов) равна:
Потребная длина нерабочей части пружины (зацепов) равна:
Деформация, сила и соответствующая вектор-сила пружины в процессе копирования рельефа поля равны:

Тогда используя выражения (5.26) и (5.40) можно определить реакцию на одном башмаке адаптера в процессе копирования рельефа поля по выражению (5.41):

Результаты силового анализа сводим в таблицу 5.3.
Таблица 5.3 – Результаты силового анализа методом мгновенных мощностей

По полученным результатам расчета строим два графика: график изменения реакции на башмаке адаптера в зависимости от обобщенной координаты (см. рисунок 5.5 а) и график изменения реакции на башмаке адаптера в зависимости от высоты копирования рельефа поля – вертикальной составляющей координаты точки (см. рисунок 5.5 б).

а)

б)
Рисунок 5.5 – Графики зависимости реакции на одном башмаке адаптера в зависимости от обобщенной координаты (а) и высоты копирования рельефа поля (б)
ДОПОЛНИТЕЛЬНОЕ ЗАДАНИЕ
1. В геометрическом анализе провести визуализацию (анимацию) трех положений смоделированного механизма уравновешивания адаптера: при максимальном и минимальном угле наклона стойки адаптера и для положения адаптера на условном горизонте. Дополнить полученную кинематическую схему условными обозначениями для одного из положений.
2. Построить на одном графике зависимости найденных в кинематическом анализе передаточных отношений в зависимости от изменения обобщенной координаты.
3. Графики реакции на башмаке адаптера дополнить ограничивающей областью допустимых значений нагрузки (маркерами) см. рисунок 5.5.
4. Провести расчет основных параметров пружины по ГОСТ 13765-86 приняв в качестве силы F1:=Fpr(jgor), F2:=Fpr(jmax). Вывести полученные результаты расчета.
5. Сделать выводы по лабораторной работе.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Назначение и принцип работы механизма уравновешивания адаптера. Классификация механизмов уравновешивания адаптеров и предъявляемые к ним требования.
2. Потенциальная энергия пружины и уравновешиваемого адаптера.
3. Что такое передаточное отношение? Порядок определения передаточных отношений при формировании математических моделей рычажных механизмов в векторном виде.
4. Основные параметры пружины и порядок их расчета.
Любое цитирование текста, использование тезисов или иллюстраций из данной статьи допускается только с указанием обязательной ссылки на первоисточник. Пожалуйста, уважайте авторские права и интеллектуальную собственность.
Данные лабораторные работы были разработаны автором в рамках преподавания курса «Математическое моделирование» на кафедре «Сельскохозяйственные машины» в ГГТУ имени П.О. Сухого в период 2005-2008 гг. для студентов дневной и заочной формы обучения. В данных лабораторных работах максимально учтены все замечания, выявленные в процессе обучения, но сохранена форма изложения материала, для передачи духа того времени.
Для цитирования данной работы | To cite this work:
Котов, А. В. Лабораторная работа №5. Разработка математической модели механизма уравновешивания адаптера / А. В. Котов // Vectormethod.blogspot.com [Электронный ресурс]. – 2020. – Режим доступа: https://vectormethod.blogspot.com/2007/01/laboratornaya-rabota-5-razrabotka-matematicheskoj-modeli-mekhanizma-uravnoveshivaniya-adaptera.html. – Дата доступа: .
Kotov A. V. Laboratornaya rabota №5. Razrabotka matematicheskoy modeli mekhanizma uravnoveshivaniya adaptera [Lab #5. Development of a mathematical model of the adapter balancing mechanism]. Vectormethod.blogspot.com [Electronic resource]. – 2020. – Mode of access: https://vectormethod.blogspot.com/2007/01/laboratornaya-rabota-5-razrabotka-matematicheskoj-modeli-mekhanizma-uravnoveshivaniya-adaptera.html. – Date of access: (in Russ.).
Ссылка на лабораторную работу №5 в формате *.pdf
Ссылка на карточки защиты лабораторной работы №5 в формате *.pdf
Комментариев нет:
Отправить комментарий